THE
HADAMARD VARIANCE
W.J. Riley, Hamilton Technical
Services
ABSTRACT
This tutorial paper is an introduction to
the Hadamard variance as it is applied for the analysis of frequency
stability. It reviews the classical Hadamard variance, describes an
overlapping version of the Hadamard variance that offers better estimates for
this statistic, introduces a modified version of the Hadamard variance, and the
newer Hadamard total variance that offers improved confidence at large
averaging factors. The setting of confidence limits and the recognition of
divergent power law noise types is also discussed.
BACKGROUND
The Hadamard [1] variance is based on the
Hadamard transform [2], which was adapted by Baugh as the basis of a
time-domain measure of frequency stability [3]. As a spectral estimator,
the Hadamard transform has higher resolution than the Allan variance , since
the equivalent noise bandwidth of the Hadamard and Allan spectral windows are
1.2337N-1t-1 and
0.476t-1 respectively [4]. For the purposes of time-domain
frequency stability characterization, the most important advantage of the
Hadamard variance is its insensitivity to linear frequency drift, making it
particularly useful for the analysis of rubidium atomic clocks [6, 7]. It
has also been used as one of the components of a time-domain multivariance
analysis [5], and is related to the 3rd structure function of phase noise [8,
21].
HADAMARD VARIANCE
The Hadamard variance is a 3-sample variance, as commonly used in the
frequency control community [6], with binomially-weighted coefficients that is
similar to the 2-sample Allan variance. It examines the 2nd difference of the
fractional frequencies, the 3rd difference of the phase variations. Because of
this, the Hadamard variance, HVAR or s²H(t), converges for the Flicker Walk FM
(a =
-3) and Random Run FM (a = -4) power-law noise types. It is also
unaffected by linear frequency drift. For frequency data, the Hadamard
variance is defined as:
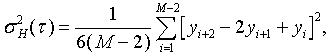
where yi is the ith of M fractional frequency values at
averaging time t.
For phase data, the Hadamard variance is defined as:
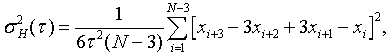
where xi is the ith of N=M+1 phase values at averaging time
t.
Like the Allan variance, the Hadamard variance is usually expressed as
its square-root, the Hadamard deviation, HDEV or
sH(t).
OVERLAPPING HADAMARD
VARIANCE
In the same way that the overlapping Allan variance makes maximum use
of a data set by forming all possible fully overlapping 2-sample pairs at each
averaging time t, the
overlapping Hadamard variance uses all 3-sample combinations [9]. It can be
estimated from a set of M frequency measurements for averaging time
t = mt0, where m is the averaging
factor and t0 is the basic
measurement interval, by the expression:
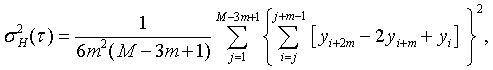
where yi is the ith of M fractional frequency values at
each measurement time.
In terms of phase data, the overlapping Hadamard variance can be
estimated from a set of N = M+1 time measurements as:
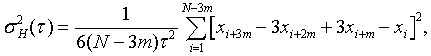
where xi is the ith of N=M+1 phase values at each
measurement time.
Computation of the overlapping Hadamard variance is more efficient for
phase data, where the averaging is accomplished by simply choosing the
appropriate interval. For frequency data, an inner averaging loop over m
frequency values is necessary. The result is usually expressed as the
square root, Hsy(t), the Hadamard deviation, HDEV. The
expected value of the overlapping statistic is the same as the normal one
described above, but the confidence interval of the estimation is better. Even
though all the additional overlapping differences are not statistically
independent, they nevertheless increase the number of degrees of freedom and
thus improve the confidence in the estimation. Analytical methods are available
for calculating the number of degrees of freedom for an overlapping Allan
variance estimation, and that same theory can be used to establish reasonable
single or double-sided confidence intervals for an overlapping Hadamard
variance estimate with a certain confidence factor, based on Chi-squared
statistics.
Sample variances are distributed according to the expression:
c²(p, df)
=(df · s²) / s²
where c² is the
Chi-square value for probability p and degrees of freedom df, s² is the
sample variance, s² is the true
variance, and df is the # of degrees of freedom (not necessarily an integer).
The df is determined by the number of data points and the noise type. Given the
df, the confidence limits around the measured sample variance are given by
s²min =
(s2 · df) /
c²(p, df), and
s²max =
(s2 · df) /
c²(1-p, df).
MODIFIED HADAMARD
VARIANCE
By similarity to the modified Allan variance, a modified version of
the Hadamard variance can be defined [17] which employs averaging of the phase
data over the m adjacent samples that define the analysis t= m·t0. In terms of phase
data, the 3-sample modified Hadamard variance is defined as:
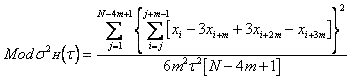
where N is the number of phase data points xi at the
sampling interval t0, and m is the averaging factor, which can extend from
1 to (floor)N/4 . This is an unbiased estimator of the modified Hadamard
variance, MHVAR. Expressions for the equivalent number of
c² degrees of freedom (edf)
required to set MHVAR confidence limits are available in [18].
Clock noise (and other noise processes) can be described in terms of
power spectral density, which can be modeled as a power law function S(fa), where f is Fourier frequency and
a is the power law exponent. When a variance such as
MHVAR is plotted on log-log axes versus averaging time, the various power law
noises correspond to particular slopes . MHVAR was developed in Reference [17]
for determining the power law noise type of Internet traffic statistics, where
it was found to be slightly better for that purpose than the modified Allan
variance, MAVAR, when there were a sufficient number of data points. MHVAR
could also be useful for frequency stability analysis, perhaps in cases where
it was necessary to distinguish between short-term white and flicker PM noise
in the presence of more divergent (a = -3 and -4)
flicker walk and random run FM noises. The MHVAR log-log slope is related to
the power law noise exponent by m = -3 - a.
The modified Hadamard variance concept can be generalized to subsume
AVAR, HVAR, MAVAR, MHVAR, and MHVARs using higher-order differences:
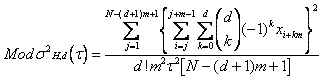
where d = phase differencing order; d = 2 corresponds to MAVAR, d = 3
to MHVAR; higher order differencing is not commonly used in the field of
frequency stability analysis. The unmodified, non-overlapped AVAR and HVAR
variances are given by setting m = 1. The allowable power law exponent for
convergence of the variance is equal to a > 1 -
2d, so the 2nd difference Allan variances can be used for a > -3 and the 3rd difference Hadamard variances for
a > -5.
HADAMARD TOTAL
VARIANCE
The Hadamard total variance, HTOT, is a total version of
the Hadamard variance. As such, it rejects linear
frequency drift while offering improved confidence at large averaging
factors.
An HTOT calculation, as described in references [15 and
19], begins with an array of N fractional frequency data points, yi
with sampling period t0 which are to be analyzed at averaging time t=mt0. HTOT is computed from a set
of N-3m+1 subsequences of 3m points. First, a
linear trend (frequency drift) is removed from the subsequence by averaging the
first and last halves of the subsequence and dividing by half the
interval. Then the drift-removed subsequence is
extended at both ends by uninverted, even reflection.
Next the Hadamard variance is computed for these 9m points. Finally, these steps are repeated for each of the N-3m+1
subsequences, calculating HTOT as their overall average.
These steps are shown in the diagram below:
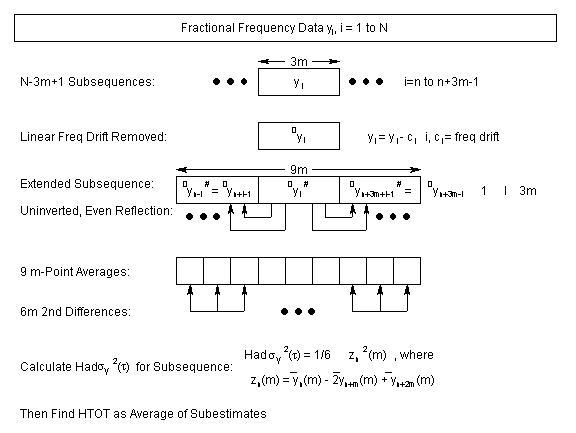
Computationally, the HTOT process requires 3 nested
loops:
·
An outer summation over the N-3m+1
subsequences. The 3m-point subsequence is formed,
its linear trend is removed, and it is extended at both ends by uninverted,
even reflection to 9m points.
·
An inner summation over the 6m unique
groups of m-point averages from which all possible fully-overlapping
2nd differences are used to calculate HVAR.
·
A loop within the inner summation to
sum the frequency averages for 3 sets of m points.
The final step is to scale the result according to the
sampling period, t0, averaging factor, m, and number of points, N. Overall, this can be expressed as:
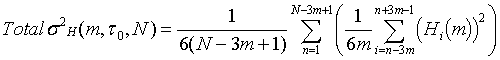
where the Hi(m) terms are the
zn(m) Hadamard 2nd differences from the triply-extended,
drift-removed subsequences. For best consistency,
the overlapping Hadamard variance is used instead of the Hadamard total
variance at m=1. At the largest possible averaging
factor, m = N/3, the outer summation consists of only one term, but the inner
summation has 6m terms, thus providing a sizable number of estimates for the
variance. The Hadamard total variance is a biased
estimator of the Hadamard variance, so a bias correction is required that is
dependent on the power law noise type and number of samples.
EXAMPLES
The following plots shown the improvement in the consistency of the
overlapping Hadamard deviation results compared with
the normal Hadamard deviation, and the extended averaging factor range
provided by the Hadamard total deviation [10].
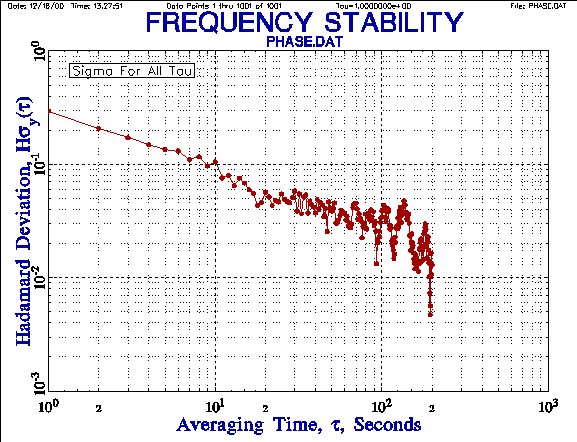
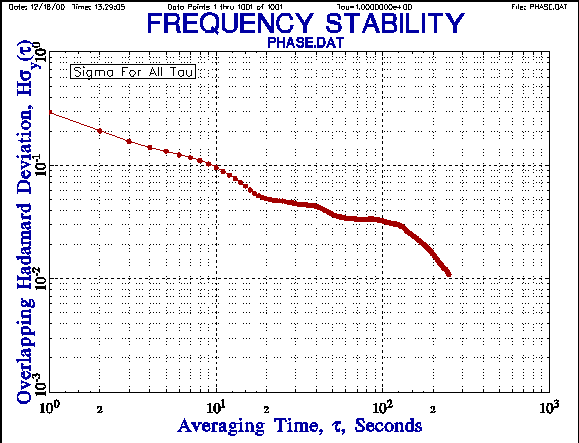
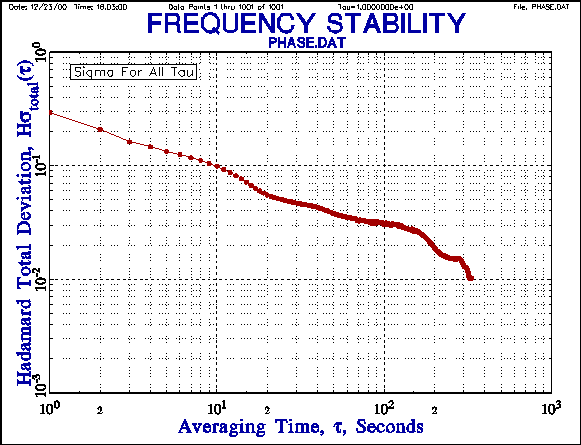
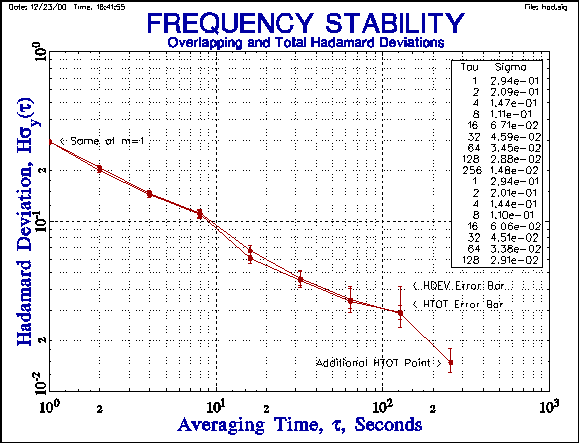
A comparison of the overlapping and total Hadamard deviations shows
the tighter error bars of the latter, allowing an additional point to be shown
at the longest averaging factor.
TRANSFER FUNCTION
The Hadamard variance sH2(t) may be related to the spectral density
of the fractional frequency fluctuations, Sy(f), by its transfer
function, |HH(f)|2:
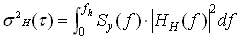
where the upper cutoff frequency, fh, is determined by
hardware factors.
The transfer function for the 3-sample (N=3) zero dead-time (T=t) binominally-weighted Hadamard variance in the frequency
domain is given by [8, 21]:
.gif)
which is plotted below:
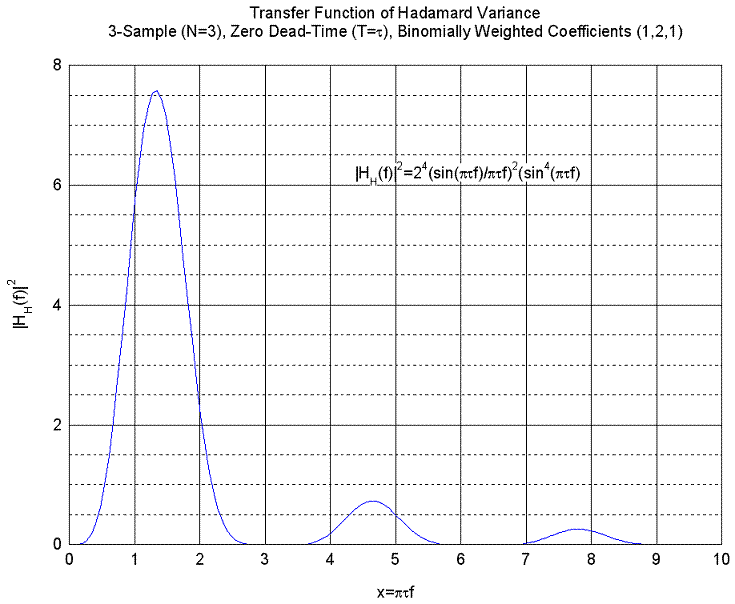
For ptf << 1, this function behaves
as (ptf)4, showing that the Hadamard
variance is convergent for power law noise processes Sya down to as low as a =
-4 (Random Run FM).
FREQUENCY DOMAIN
ANALYSIS
The Hadamard variance may also be used to perform a frequency domain
(spectral) analysis because it has a transfer function that is a close
approximation to a narrow rectangle of spectral width of
1/(2·N·t0), where N is the
number of samples, and t0
is the measurement time [16]. This leads to a simple expression for the spectral
density of the fractional frequency fluctuations Sy(f) » 0.73 ·
t0· s2H(t)
/ N, where f =
1/(2·t0), which can be
particularly useful at low Fourier frequencies.
OTHER SIMILAR
VARIANCES
The Picinbono variance is a similar 3-sample statistic. It is
identical to the Hadamard variance except for a factor of 2/3 [12, 13,
20]. Sigma-z is another statistic that is similar to the Hadamard
variance that has been applied to the study of pulsars [14].
NOISE IDENTIFICATION AND
CONFIDENCE LIMITS
It is necessary to identify the dominant
power law noise type as the first step in determining the estimated number of
chi-squared degrees of freedom for the Hadamard statistics so their confidence
limits can be properly set [11, 15]. Because the
Hadamard variances can handle the divergent flicker walk FM and random run FM
power law noises, techniques for those noise types must be
included. Noise identification is particularly
important for applying the bias correction to the Hadamard total variance.
REFERENCES
1.
Jacques
Saloman Hadamard (1865-1963), French mathematician.
2.
W.K. Pratt, J. Kane and H.C. Andrews, "Hadamard Transform Image Coding",
Proc. IEEE, Vol. 57, No. 1, pp.38-67, January 1969.
3.
R.A. Baugh,
"Frequency
Modulation Analysis with the Hadamard Variance", Proc. Annu. Symp. on
Freq. Contrl., pp. 222-225, June 1971.
4.
K. Wan, E. Visr and J. Roberts,
"Extended
Variances and Autoregressive Moving Average Algorithm for the Measurement and
Synthesis of Oscillator Phase Noise", 43rd Annu. Symp. on Freq.
Contrl., pp.331-335, June 1989.
5.
T. Walter,
"A
Multi-Variance Analysis in the Time Domain", Proc. 24th PTTI
Meeting, pp. 413-424, December 1992.
6.
S.T. Hutsell,
"Relating the
Hamamard Variance to MCS Kalman Filter Clock Estimation", Proc.
27th PTTI Meeting, pp. 291-302, December 1995.
7.
S.T. Hutsell,
"Operational Use
of the Hamamard Variance in GPS", Proc. 28th PTTI
Meeting, pp. 201-213, December 1996.
8.
J. Rutman,
"Oscillator
Specifications: A Review of Classical and New Ideas", 1977 IEEE
International Freq. Contrl. Symp., pp.291-301, June 1977.
9.
This expression for the overlapping Hadamard variance was developed by
the author at the suggestion of G. Dieter and S.T. Hutsell.
10.
These plots were produced by the
Stable32 program from Hamilton
Technical Services.
11.
Private communication, C. Greenhall to W. Riley, 5/7/99.
12.
B. Picinbono, "Processus a Accroissements Stationnaires", Ann. des
telecom, Tome 30, No. 7-8, pp. 211-212, July-Aug, 1975.
13.
E. Boileau and B. Picinbono, Statistical Study of Phase Fluctuations and
Oscillator Stability, IEEE Trans. Instrum. Meas., IM-25, No. 1, pp.
66-75, March 1976.
14.
D.N. Matsakis and F.J. Josties,
"Pulsar-Appropriate
Clock Statistics", Proc. 28th PTTI Meeting, pp. 225-236,
December 1996.
15.
D. Howe, R. Beard, C. Greenhall, F.
Vernotte, and W. Riley, "A
Total Estimator of the Hadamard Function Used For GPS Operations", Proc.
32nd PTTI Meeting, Nov. 2000, pp. 255-268.
16.
Chronos Group, Frequency
Measurement and Control, Section 3.3.3, Chapman & Hall, London, ISBN
0-412-48270-3, 1994.
17. S. Bregni and L. Jmoda,
"Improved
Estimation of the Hurst Parameter of Long-Range Dependent Traffic Using the
Modified Hadamard Variance", Proceedings of the 2006 IEEE International
Conference on Communications (ICC 2006), June 2006 .
18. 2. C.A. Greenhall and W.J. Riley,
"Uncertainty of
Stability Variances Based on Finite Differences", Proc. 35th PTTI
Meeting, December 2003.
19. D.A. Howe, R.L. Beard, C.A. Greenhall, F. Vernotte,
W.J. Riley, and T.K. Peppler,
"Enhancements
to GPS Operations and Clock Evaluations Using a "Total" Hadamard
Deviation", IEEE Trans. Ultrason. , Ferroelect., Freq. Contr., Vol. 52,
No. 8, August 2005, pp. 1253-1261.
20. J.J Gagnepain,
"La
Variance de B. Picinbono", Traitement du Signal, Vol. 15, No. 6,
Special, 1998, pp. 477-482.
21. J. Rutman, "Characterization of Phase and Frequency
Instabilities in Precision Frequency Sources", Proc. IEEE, Vol. 66, No.
9, September1978.
Last Rev. 05/12/07
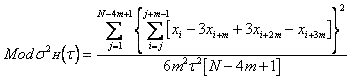
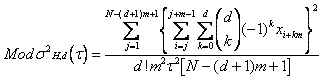





.gif)